Skip to content

The Sampling Theory

The sampling theory describes how continuous signals can be sampled and reconstructed accurately from their discrete samples, provided certain conditions are met.

Key Concepts

Sampling

Sampling involves measuring a continuous-time signal \( x(t) \) at discrete intervals, resulting in

\[ x[n] = x(nT_s) \]

where:

  • \( T_s \): Sampling period or sampling interval.
  • \( f_s = \frac{1}{T_s} \): Sampling frequency (samples per second).

Nyquist-Shannon Sampling Theorem

A continuous signal can be perfectly reconstructed from its samples if the sampling frequency \( f_s \) is greater than twice the highest frequency component \( f_{\text{max}} \) of the signal:

\[ f_s > 2 f_{\text{max}} \]

Nyquist frequency

\( f_{\text{Nyquist}} = \frac{f_s}{2} \), the maximum frequency that can be accurately represented with a given sampling rate.

Aliasing

If \( f_s \leq 2 f_{\text{max}} \), higher frequency components appear as lower-frequency artifacts in the sampled signal, distorting the reconstructed signal. This phenomenon is called aliasing.

Reconstruction

  • If \( f_s > 2 f_{\text{max}} \), the original signal \( x(t) \) can be reconstructed perfectly using an ideal low-pass filter with a cutoff frequency equal to \( f_{\text{Nyquist}} \).

Key Relationships

  1. Sampling Frequency \( f_s \):

    • Determines how often the signal is sampled.
    • A higher \( f_s \) allows for capturing higher frequencies and more detail.

  2. Reconstructed Signal Frequency:

    • After reconstruction, frequencies up to \( f_{\text{Nyquist}} \) are preserved accurately.
    • Frequencies above \( f_{\text{Nyquist}} \) are aliased.

Example

Using calculus

  • Consider a signal with a maximum frequency \( f_{\text{max}} = 1 \, \text{kHz} \):

  • Minimum Sampling Rate: \( f_s > 2 \times 1 \, \text{kHz} = 2 \, \text{kHz} \).

  • If sampled at \( 4 \, \text{kHz} \), the signal can be perfectly reconstructed.
  • If sampled at \( 1.5 \, \text{kHz} \), aliasing occurs, and the original signal cannot be accurately reconstructed.

Using an image

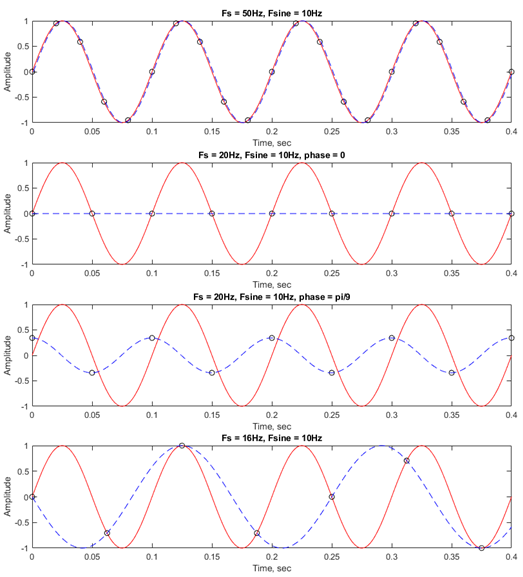
Conclusions of sampling around Nyquist Rate - Stack Exchange

Practical Considerations

  1. Anti-Aliasing Filter

    • Used before sampling to remove frequencies above \( f_{\text{Nyquist}} \), preventing aliasing.

  2. Oversampling

    • Sampling at a rate significantly higher than \( 2 f_{\text{max}} \) can improve practical reconstruction by reducing noise sensitivity.