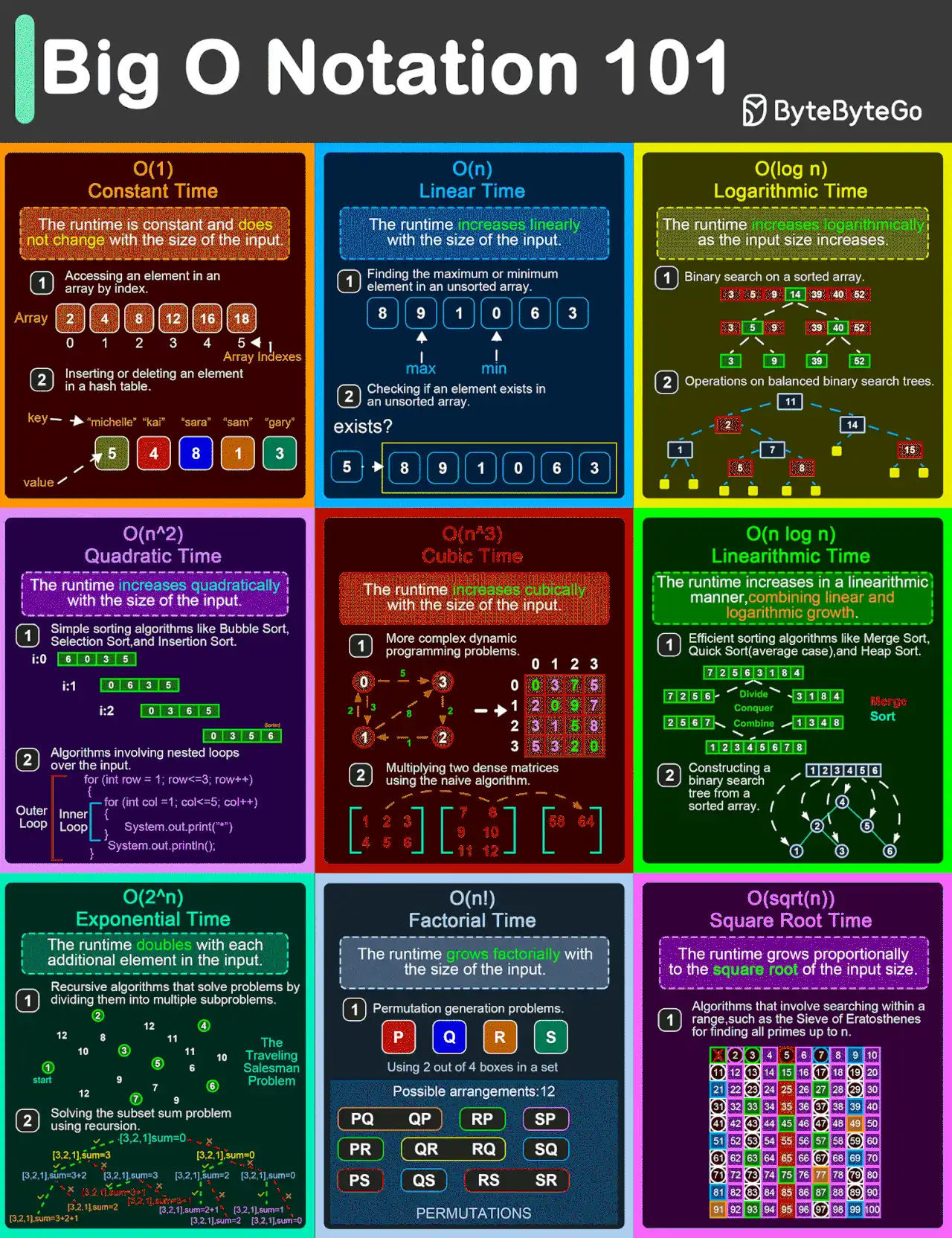
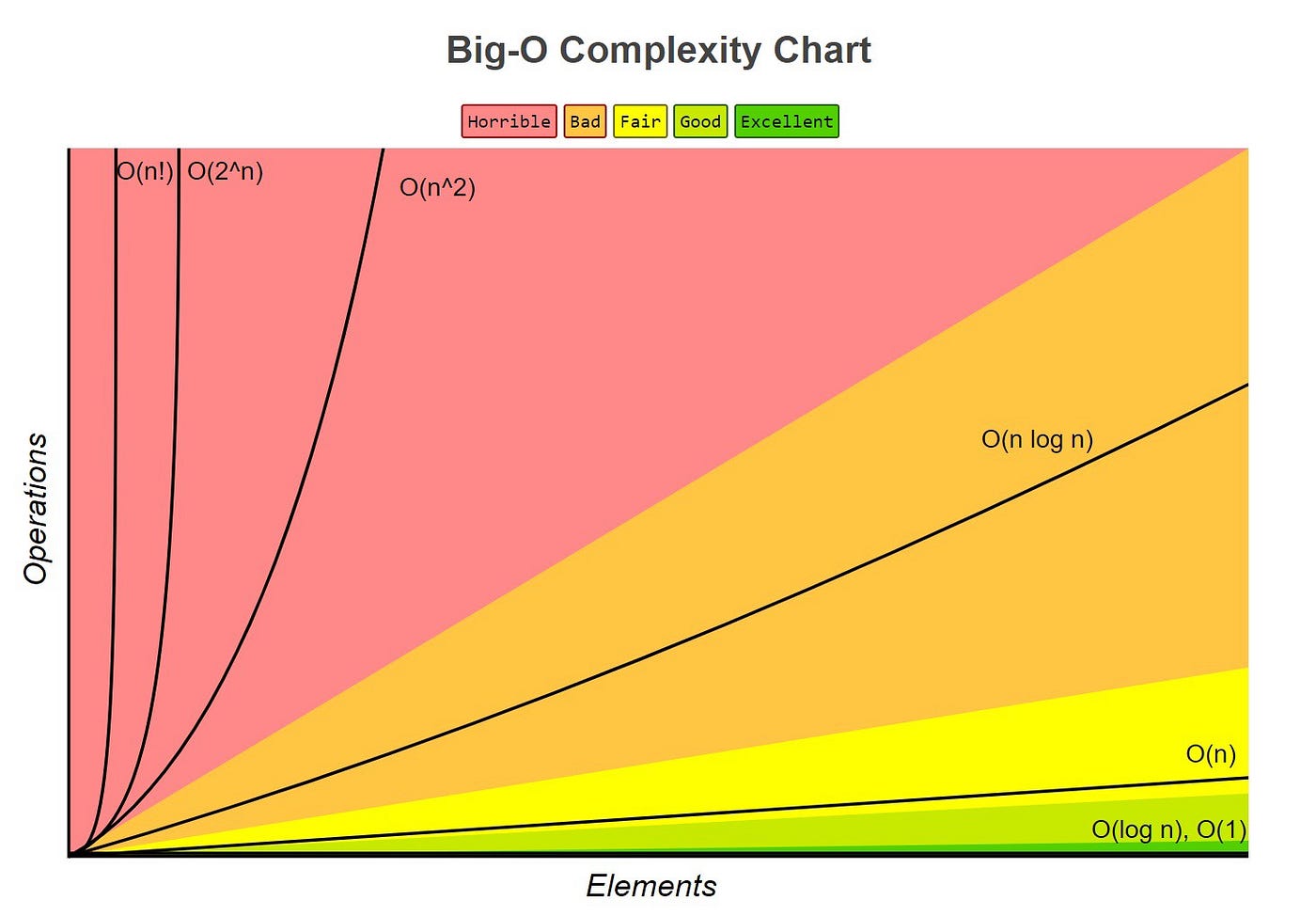
Big O Notation
Explanation
-
O(\(1\))
This is the constant time notation. The runtime remains steady regardless of input size. For example, accessing an element in an array by index and inserting/deleting an element in a hash table.
-
O(\(n\))
Linear time notation. The runtime grows in direct proportion to the input size. For example, finding the max or min element in an unsorted array.
-
O(\(log(n)\))
Logarithmic time notation. The runtime increases slowly as the input grows. For example, a binary search on a sorted array and operations on balanced binary search trees.
-
O(\(n^2\))
Quadratic time notation. The runtime grows exponentially with input size. For example, simple sorting algorithms like bubble sort, insertion sort, and selection sort.
-
O(\(n^3\))
Cubic time notation. The runtime escalates rapidly as the input size increases. For example, multiplying two dense matrices using the naive algorithm.
-
O(\(n log(n)\))
Linearithmic time notation. This is a blend of linear and logarithmic growth. For example, efficient sorting algorithms like merge sort, quick sort, and heap sort
-
O(\(2n\))
Exponential time notation. The runtime doubles with each new input element. For example, recursive algorithms solve problems by dividing them into multiple subproblems.
-
O(\(n!\))
Factorial time notation. Runtime skyrockets with input size. For example, permutation-generation problems.
-
O(\(\sqrt{n}\))
Square root time notation. Runtime increases relative to the input’s square root. For example, searching within a range such as the Sieve of Eratosthenes for finding all primes up to n.